Sketchpad in the Middle Grades

Middle school marks the transition from concrete to abstract mathematical concepts and objects. Students must work with negative numbers, variables, and increasingly formal definitions of geometric shapes and their properties.

As students cross the bridge connecting “shape and number” to “geometry and algebra,” they are often wary of the manipulatives they used in elementary school, which may seem childish to them. At the same time, they stand to benefit from manipulatives more than ever during this period of their mathematical growth. For teachers, middle school presents a wider range of topics to address than either elementary or secondary school, and often a wide range of mathematical backgrounds in incoming students. Sketchpad provides an ideal toolbox of sophisticated manipulatives that encourage students to make increasingly abstract topics visual and tangible, through construction, exploration, prediction, and conjecture. Sketchpad can become a tool that teachers return to often during the year, and that students can count on for support and personalized insight.

Geometry: Construction and Transformation

Middle school mathematics draws on all of the core mathematics menus in Sketchpad—Construct, Transform, Measure, Number, and Graph—but often requires only basic levels of interaction with them.

Starting with geometry, students can use the basic tools in the Toolbox to create and manipulate points, circles, and lines. Then, turning to the Construct menu, they find equivalent construction commands (such as Line and Circle by Center+Point) for making the same shapes, with a more formal emphasis on vocabulary and definition. From there, they can learn constructions such as parallel and perpendicular lines and angle bisectors.

Students use the Transform menu to make rotations, reflections, and translations of shapes, explore the properties of these isometries, and perhaps even create a tessellation. Dragging their shapes generates a wide range of examples, lets students evaluate the validity of their own constructions, focuses attention on properties, and shows support for—or counterexamples to—many possible conjectures.

Measurement and Conjecture

Moving from shape to number, the Measure menu introduces angle, area, and perimeter measurements. Because measurements in Sketchpad are dynamic, a measurement that does not change when shapes are dragged frequently represents an important relationship or property.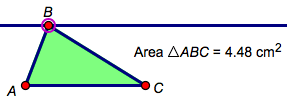

For example, dragging one vertex of a triangle along a line parallel to its base demonstrates that the measured area of the triangle remains unchanged, because the base and height are unchanged. The Calculator (in the Number menu) becomes an important tool for comparing multiple measurements, often by finding their sum or their ratio. For example, when students calculate the sum of the angle measures in a triangle and then drag the vertices, they quickly become convinced of the invariance of the sum, even as individual angles rapidly change.

Graphing and Algebra

Both shape and number find new relationships on the coordinate plane, which can be introduced from the Graph menu. As a gentle introduction, have students drag a point around the plane while measuring its coordinates, and ask them to describe how the abscissa and ordinate (x and y) values reflect their point’s position. Have them search for patterns: Where is the abscissa 0? Where is it 1? Where is it equal to the ordinate? Later, try a similar experiment with slope. Measuring the slope of a line on the plane, and experimenting with dragging that line, provides students an important visual understanding of how the numeric slope value changes with perceived steepness.

You can also explore the Sample Activities to find dynamic, visual Sketchpad models that target a variety of algebraic topics, including properties of operations, solving equations, and interpreting graphs.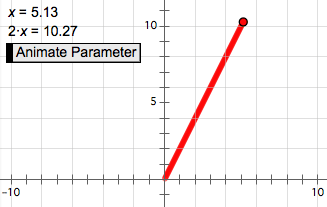

Simple algebraic models can be built from scratch using the Number menu and Calculator. A parameter in Sketchpad (in the Number menu) is a named, changeable value, and therefore acts as an accessible introduction to the idea of a variable in algebra. For example, create a new parameter x = 3, and then calculate 2 • x (that is, 6). Now change the value of the parameter from 3 to 4, and have students describe the dependent relationship of 2 • x to the “varying” parameter. As an extension, select the parameter and the calculation and choose Graph | Plot as (x, y) to plot point (x, 2 • x). Then have students animate the parameter (turning it into a variable) and describe how that point moves as x varies.

The dynamic and visual nature of Sketchpad allows students to develop concrete meanings for the formulas, symbols, and abstractions they encounter, and often elicits from them “Now I get it!” feelings of relief and delight. In moving back and forth between shape and number, students can begin to see the highly interconnected nature of mathematics, and appreciate its appeal and power.

Sample Activities

Back to Sketchpad in the Classroom