 Tracing the Slope Function: Animate a Secant Line
Tracing the Slope Function: Animate a Secant Line
For a linear function, like f(x) = 2x – 3, you can calculate the slope by picking two points and applying the slope formula. But what happens when you try to find the slope of a function that isn’t linear, like f(x) = sin(x)? In this tutorial, you’ll gain some intuition about functions whose slopes are not constant and begin to examine some of the fundamental concepts of calculus. Don’t worry if you’re not familiar with calculus; there is still plenty to explore.
Measure a Changing Slope 
You’ll start by plotting a sine function, f(x) = sin(x), and constructing a secant line on its graph. Then you’ll measure the slope of the secant line and observe how the slope varies as the line moves along the function plot.
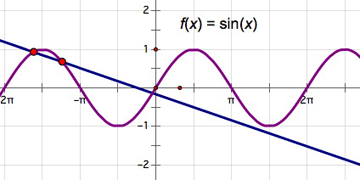
In a new sketch, choose Graph | Plot New Function. Type sin(x) in the Calculator and click OK. Click Yes to switch angle units from degrees to radians.
Press and hold the Segment tool icon until a pop-out menu appears. Choose the Line tool.
Construct a secant line to the function plot by clicking two places fairly near each other on the sine graph.
Select the secant line and choose Display | Animate Line. The secant line begins to move along the graph.
Use the Pause button on the Motion Controller to pause and restart the movement. Use the up and down arrows on the Motion Controller to change the speed of the animation.
Describe the motion of the secant line. What changes as it moves from left to right? What happens when the points reach the edge of the screen? What else do you notice?
Pause the movement of the line. Deselect all objects by clicking in empty space. Select the secant line and choose Measure | Slope.
What does this measurement represent? What do you observe about it as the line moves? What are the largest and smallest values you observe? Where do they occur?
Plot and Trace a Point 
You will now graph the slope measurement to help you understand its behavior.
Select point A and choose Measure | Abscissa (x). (If the line is moving, you can select point A by pressing the Target area of the Motion Controller and choosing point A from the menu.)
Select, in order, the independent variable (xA) and the dependent variable (Slope AB) and choose Graph | Plot as (x, y).
If the line is not moving, set it back in motion. Observe the behavior of the plotted point. How does it move horizontally? How does it move vertically?
Pause the movement of the line. With the plotted point selected, choose Display | Trace Plotted Point. Restart the movement.
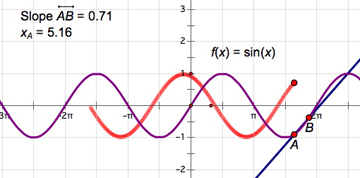
As the plotted point moves, it leaves a trace. Describe this trace. Watch if for several trips back and forth, and describe everything that you observe. Describe what happens when points A and B reach either edge of the screen.
Make Action Buttons 
Finally, you’ll create an Animation button and a Movement button to further explore your model.
Click Stop in the Motion Controller to stop the animation. Erase the trace of the plotted point by choosing Display | Erase Traces. Then, drag points A and B so that they are very close together.
Select points A and B. and choose Edit | Action Buttons | Animation. Leave the default settings and click OK.
Press the Animate Points button several times to start and stop the animation. Describe the trace that you see now. What are its maximum and minimum values? Does this trace resemble any function you know?
Stop the animation. Select in order points B and A and choose Edit | Action Buttons | Movement. Leave the default settings and click OK.
Press the Move B → A button. What happens? Why?
Move one of the points so they’re slightly separated and restart the animation.
Explore More
The derivative of f(x) = sin(x) gives you the precise slope of the sine function at every point along the curve. Select the equation f(x) = sin(x) and choose Number | Define Derivative Function. The derivative, f′(x), appears. Use Sketchpad’s Calculator to compute f′(xA). Then plot the point (xA, f′(xA)). Trace the point and press the Animation button to create a function representing the slope of f(x) = sin(x) at every point along the curve.