Trigonometry, Conics, and Precalculus

As students progress from elementary algebra to trigonometry, conics, and precalculus, building and exploring dynamic models in Sketchpad helps them consolidate the abstractions introduced in algebra, learn important new concepts, and prepare for the exciting step to calculus. Sketchpad’s ability to provide both geometric and algebraic representations as dynamic systems gives students the visualization tools they need to make connections between geometry and algebra as they generalize the concepts of variables and functions, apply trigonometry and conics to real-world problems, and deepen their understanding of slope and average rate of change.

Trigonometry

An excellent starting point for the exploration of trigonometry is to build a sine wave tracer that joins the linear motion of a point moving along a line with the circular motion of a point moving around a circle. By joining these two motions into the coordinates of a point, students create a model of a sine curve and develop deep insight into the nature of a periodic function.

It’s a short step from this purely geometric model to an algebraic model. Students can select the circle, choose Graph | Define Unit Circle, and then choose Graph | Grid Form | Trigonometric Axis. Plotting the “height” of the point on the circle (the y-value of point D) as a function of the point’s distance around the circle’s circumference, and then constructing the locus of the plotted point, students make a powerful connection between the geometry of the unit circle and the trigonometry of the sine wave.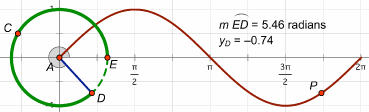

As with the linear, quadratic, and exponential functions in algebra, students can vary the coefficients of a trigonometric equation using parameters or sliders to develop an understanding of how scaling and translation impacts the function plot. As students edit their parameters to transform a parent function, they not only learn to transform trigonometric functions, they solidify their understanding of how functions transform input into output, and of how transformations, functions, and mappings are different ways to represent mathematical relationships.

Another powerful connection that Sketchpad makes tangible for students is the relationship between right triangle and unit circle trigonometry. Students can start with a unit circle, construct a right triangle with a vertex on the circle, and explore the connections between first quadrant right triangle trigonometry and the expanded realm of trigonometric functions.

Conics

With Sketchpad, students can construct conic sections from their geometric definitions and make connections between their representations on the coordinate plane and their equations. Start by constructing a segment with one endpoint on a line, and then constructing its perpendicular bisector. Then select the segment endpoint and the perpendicular line and choose Construct | Locus. The locus of bisectors forms a parabola: the line is the directrix and the free endpoint of the segment is the focus. Students can construct and manipulate parabolas using both geometric and algebraic definitions, and explore the connections between the two.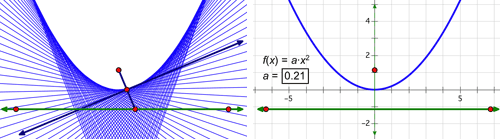

Now modify the geometric construction by placing one endpoint of the segment on a circle instead of a line and repeat the process to form a hyperbola. Then drag the focus—the free endpoint of the segment—inside the circle and see the locus transform to form an ellipse, or even a circle. Explore the Sample Activities to see how you might introduce analytic conics to students.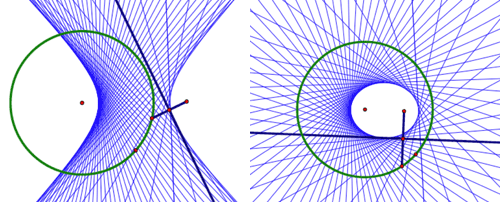

With Sketchpad, students are able to extend the connection between algebra and geometry beyond the fundamental algebraic activity of graphing a function, and delve more deeply into the analytic geometry of how the symbolic and graphical forms of conics are related.

Precalculus

Sketchpad allows students to explore the vast scope of topics that are typically part of a precalculus course, including composition and inverses of functions, vectors and matrices, polar coordinates, complex numbers, sequences and series, and the conceptual underpinnings of calculus itself. While some of these topics can be explored easily using basic Sketchpad commands, some require prepared models, available in the Sample Activities or by choosing Help | Sample Sketches & Tools.

One particularly powerful model allows you to simultaneously view a Cartesian graph and a polar graph, and watch as the corresponding points move along their plots in the two different coordinate systems. Seeing the two animated representations together allows students to make sense of the relationship between them. Other prepared models allow students to work with vectors, matrix operations and transformations, complex numbers, and series.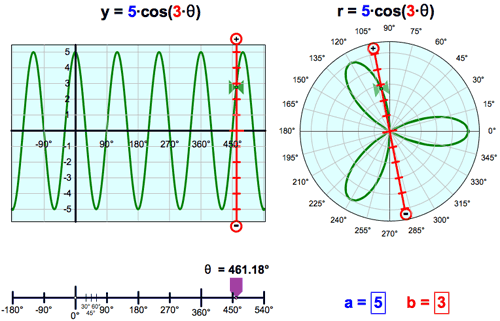

In preparation for calculus, students can also explore the relationship between the slope of a line tangent to a function at a point and the derivative of the function at that point. Use Graph | Plot New Function to plot any nonlinear function and construct a secant line using two points on the function plot. As you bring the two points closer together, the secant line approximates the tangent line, and its slope approximates the derivative. Students can then plot a point with the same x-coordinate as a point on the function plot and a y-coordinate based on the slope value.

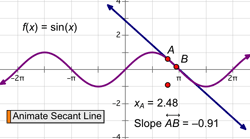When students animate the secant line, the plotted point traces an approximation of the derivative function. These tangible and visual experiences in Sketchpad help students build the conceptual underpinnings that will prepare them to develop a deep understanding of and appreciation for calculus.

Sample Activities

Back to Sketchpad in the Classroom