
 
 |
Authoring Your Own Sketchpad ActivitiesSketchpad makes it nearly irresistible to take some of your favorite mathematical activities and make them even better by turning them into Sketchpad-based lessons. Here are a few big ideas to keep in mind to take maximum advantage of the software. Make a sketch dynamic to take full advantage of Sketchpad.Nicholas Jackiw, Sketchpad’s designer, likes to point out that for all the power of the program, “Sketchpad revolves around just one essential idea—Dynamic Geometry. Simply put, Dynamic Geometry operates under the principle that mathematics in motion is intrinsically more interesting than static mathematics, and that the mathematical behaviors that Sketchpad images exhibit when you drag them yield powerful insights.” As you design Sketchpad activities for students, whether they are geometric, algebraic, or focused on other content, keep this idea in mind and strive to make your sketches as dynamic as possible. If nothing moves on Sketchpad’s screen as a student works through your activity, you have not used the potential of Sketchpad. Sketchpad is about more than geometry.The dynamic principles of Sketchpad can be applied to nearly any area of mathematics, from number concepts in elementary mathematics to topics in calculus and beyond. Whether it be an array model of the distributive property or an interactive model of a tangent line to a function, think of Sketchpad as a suite of tools for promoting visual expression of mathematical ideas. Look at the Sample Activities to see how Sketchpad can be used to investigate a broad range of content. Keep the storyline about mathematics and not about Sketchpad.Avoid the trap of saying too much about Sketchpad and too little about the mathematical concepts you want students to explore. For instance, to instruct students how to construct an equilateral triangle you could write:
While this is a perfectly clear and useful set of directions for operating Sketchpad, it omits the big mathematical ideas. Instead, you could write:
Depending on your students’ experience, you could follow with specific Sketchpad hints, or you could encourage students to confront and solve this mathematical problem on their own, using Sketchpad as their tool. Don’t have all the fun yourself!Once you begin authoring your own Sketchpad activities, you’ll see how satisfying it is to express mathematical ideas through the sketch-building process. Share this experience with students and give them the opportunity to construct Sketchpad models of their own. Students are naturally inquisitive and love the ability to take an idea or conjecture and turn it into a dynamic and compelling model to share with their classmates. Building Sketchpad models makes mathematics more memorable and meaningful to students because they are asking and exploring their own questions. You can also share your sketches, and ones your students have made, with other Sketchpad users at Sketch Exchange. |
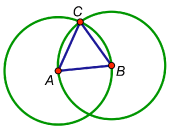 Use the Compass tool to construct a circle. Label the center A. Label the radius point B. Now use the Compass tool to construct a second circle with center B and radius point A. Use the Point tool to create a point at the intersection of the two circles. Label the point C. Use the Segment tool to connect the three points to form a triangle.
Use the Compass tool to construct a circle. Label the center A. Label the radius point B. Now use the Compass tool to construct a second circle with center B and radius point A. Use the Point tool to create a point at the intersection of the two circles. Label the point C. Use the Segment tool to connect the three points to form a triangle.