
 
 |
Calculus and BeyondBecause Sketchpad’s functionality focuses on fundamental mathematical objects and operations, there’s no upper bound to the type of mathematics you can explore and model. Sketchpad can offer unique insight into any topic for which mathematical visualization is relevant—classical and modern geometries, graphing, complex analysis, statistical charts and diagrams, physical simulations, topology, and so on—with its connection between direct manipulation and continuous visualization. CalculusSketchpad excels at modeling and illustrating many ideas based on graphical analysis, beginning with a core idea of calculus: at a sufficiently small scale, almost everything appears linear.
Similar dynamic visualizations—of numeric integration through Riemann sums, or of slope fields and differential equations—repeatedly demonstrate how continuous calculus definitions emerge from finite processes taken to the limit as key distances approach zero. With Sketchpad, students can build and see these physical representations—and they can see how formal definitions emerge by reasoning from a few successive approximations, through a few dozen, and then through hundreds or thousands of better approximations all approaching the limit. This experience gives them a concrete image—and an accessible, tangible process for extending it—as the foundation for more abstract concepts and definitions. Importantly, in many dynamic models of general definitions, the exact equation of a function is less important than its relation to other objects in the model. For example, if f' is the derivative of f, then f'(x0) determines the slope of the tangent to f at x0 whether f is defined as 2x or x2 or sin x. Therefore, repeatedly changing a function’s expression in a Sketchpad model can allow you to see or demonstrate how that single model applies to an entire class of mathematical behaviors. (As a shortcut to Edit | Edit Function, just double-click a function. Think of editing a function’s equation as calculus’s dynamic equivalent of dragging an independent point in elementary geometry!) The common Sketchpad tools used in calculus are the basic geometry tools of the Toolbox and the Construct menu, combined with functions (Graph | New Function), their numeric evaluation for specific or calculated x-values (via the Calculator), and their graph on a given coordinate system (Graph | Plot Function). In addition, Sketchpad contains a computer algebra system capable of symbolic differentiation (Number | Define Derivative Function). Like other functions, derivative functions in Sketchpad are dynamic: change the function they differentiate, and they’ll change as well. You may also find use for Number | Define Function from Drawing, which allows you to turn a freehand sketch of a function’s graph (that you’ve made with the Marker tool) into a graphable, numerically evaluatable, and fully differentiable form. Prepared ModelsThere are many excellent prepared sketches and activities for use in the calculus classroom—see the Sample Activities and Help | Sample Sketches & Tools for some examples. At the same time, though, insist that students try some of simpler activities and constructions themselves. Hands-on experience is the best way to ensure that students don’t pass through an entire course without realizing that calculus is a topic fundamentally concerned with thinking about shape rather than with just functions and formulae! Beyond CalculusThe mathematical landscape beyond calculus is wide open for Sketchpad-based exploration. Easy access to this landscape will require mastery of Sketchpad basics: construction, transformation, calculation, and measurement, and moving fluidly between geometric or visual representations and numeric or symbolic calculations. You’ll also need to become familiar with some of the more advanced operations Sketchpad offers for generalizing, reusing, and encapsulating mathematical definitions or relationships. Just as a function encapsulates an entire set of numeric coordinate relations through an equation, a locus encapsulates an arbitrary set of geometric relationships into a continuum of proximate positions. The number of new shapes and classes of geometric objects you can build through locus definition is unlimited. (Loci in Sketchpad come in two flavors—geometric and parametric—and are accessed through the Construct menu.) Once you’ve defined a new shape or object by construction, consider turning it into a new tool or a new “primitive object” in the program by creating a custom tool to repeat the construction as needed. (And if it’s the sort of tool you want to use every day, install it in your Tool Folder.) One of the foundational elements of mathematical representation and development is the interplay between the geometric and the arithmetic; another is the tension between the continuous and the discrete. At a basic level, dragging a point in Sketchpad is a continuous form of variation, while editing a parameter k from one numeric value to another is a discrete change. Adjusting parameter values by dragging or animating blurs this distinction. At a more advanced level, where locus is a mathematical tool for building new ideas by encapsulating continuous change (across some domain), iteration is a powerful tool for encapsulating discrete change and repetition. As you learn how to use Sketchpad’s Transform | Iterate command, you’ll realize it’s not just a novelty for generating fractal imagery, but a powerful building block for counting, summing, sequences, series, and other algorithmic repetitions. Custom transforms, parametric color, and Hot Text also all have their place in any advanced mathematical survey of Sketchpad functionality: custom transforms allow you to define new (and nonlinear) transformations of objects; parametric color opens up an entire new dimension of visualization beyond the 2-dimensions of Sketchpad’s plane and the third dimension of Dynamic Geometry variation in time (put together, they can create custom color transforms or color surface plots); and Hot Text, combined with mathematical formatting operations from the Text Palette, can be used to create new or advanced symbolic notations of measurements and mathematical forms that Sketchpad itself does not natively support (for example, the standard or polar form of complex coordinates, or vector notation in linear algebra). You can learn about how to use these features by reading relevant entries in the Reference Center. The Advanced Sketch Gallery
If you develop interesting upper-level mathematics materials of your own in Sketchpad, consider contributing them to the Advanced Sketch Gallery for others! |
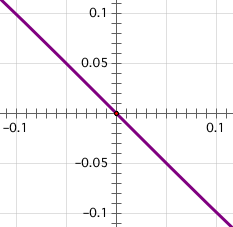 For example, choose Graph | Plot New Function and plot a nonlinear function that passes through the origin, perhaps
For example, choose Graph | Plot New Function and plot a nonlinear function that passes through the origin, perhaps 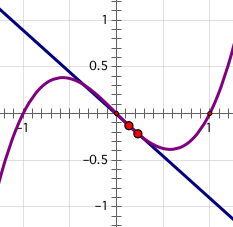 Motivate the derivative through the realization that ∆x can’t actually be zero for purely geometric reasons: two points define a line. But if ∆x were zero, A and B would be the same point—and so the secant would no longer be defined.
Motivate the derivative through the realization that ∆x can’t actually be zero for purely geometric reasons: two points define a line. But if ∆x were zero, A and B would be the same point—and so the secant would no longer be defined.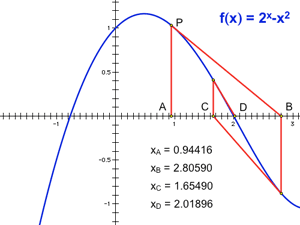 The benefit of a good prepared sketch can’t be overestimated. It can take the better part of a class period to introduce Newton’s method at the blackboard and demonstrate its first few iterates on the graph of a simple function. But in half the time, you can cover the same material with a prepared sketch, and go much further—by continuing to the hundredth iterate, or the 10,000th; by varying your initial starting point and seeing how that influences the basin of convergence; or by changing the function’s coefficients and even its symbolic form to explore how other functions (or families of functions) respond to the method.
The benefit of a good prepared sketch can’t be overestimated. It can take the better part of a class period to introduce Newton’s method at the blackboard and demonstrate its first few iterates on the graph of a simple function. But in half the time, you can cover the same material with a prepared sketch, and go much further—by continuing to the hundredth iterate, or the 10,000th; by varying your initial starting point and seeing how that influences the basin of convergence; or by changing the function’s coefficients and even its symbolic form to explore how other functions (or families of functions) respond to the method. You can
You can