
 
 |
Geometry with SketchpadGeometry is “home base” in Sketchpad. Starting with the toolbox, you’ll find the Point, Straightedge (line), and Compass (circle) tools—the building blocks of Euclidean geometry, and the starting points for rich explorations in school geometry and beyond. Use the Straightedge tool to draw a triangle, and then drag one of the vertices of that triangle using the Arrow tool to create an infinite variety of triangles. This simple introduction to Sketchpad helps build a rich conception of the triangle—so that students might not expect them all to have horizontal bases! Dragging allows students to see the continuous variations that are possible in geometric shapes, and to build visual and spatial imagery that will help them become better problem solvers. As students attempt to configure their triangles into, say, isosceles ones, you can develop the distinction between drawing and constructing. Simple drawing is useful in focusing attention on properties, while constructing allows the creation of robust and precise shapes, which can then be used in future geometric explorations.
ConstructionAfter becoming familiar with Sketchpad’s toolbox, students can use the Construct menu to focus on constructing shapes that involve increasingly sophisticated properties and relationships. They can constructing midpoints and intersections, and parallel and perpendicular lines. The menu itself helps direct attention to the requirements of such constructions. For example, the Construct | Perpendicular Line command will be grayed out until the appropriate foundational objects are selected—a perpendicular line must pass through a given point and be perpendicular to some other line, so a point and a line must be selected. The commands in the Construct menu can be used to construct the range of special triangles, quadrilaterals, and other polygons that are studied in geometry. But more importantly, once a shape such as a kite has been constructed, students can begin to look for invariances and generalizations. What do you notice when you draw the diagonals of the kite? When you drag the vertices of the kite, what stays invariant about the diagonals? Are there any counterexamples? Also in the Construct menu, you’ll find the Locus command. Loci are some of the most powerful mathematical objects in Sketchpad, and let you create geometric objects with any mathematical properties you desire. Though often neglected in school curriculum, loci were very important in the study of classical geometry, and locus-based definitions and proofs remain common in advanced geometric contexts. TransformationThe Transform menu allows students to explore reflection, rotation, translation, and dilation. Once again, the menu commands help make students aware of the properties that define each transformation—reflections can’t be done without first specifying a line of reflection. In addition to creating appealing symmetric designs, students can use Sketchpad’s dynamic capabilities to understand the geometric properties of these transformations. Ask students to draw a shape and reflect across a vertical line. Then, drag a point on the original shape and see what happens to the image point. Now move the whole line of reflection and observe. Predicting and observing the effects of manipulations like these helps students understand geometric properties while also gaining spatial awareness. The Iterate command can be used to create fractals, as well as a range of other constructions that can be defined in an iterative manner. For example, a hexagon can be constructed by rotating a point around a center by 60° repeatedly—you can do that rotation once, then iterate the procedure. Students may find iteration useful for some investigations, and you might also use it to build sketches that can be used to explore questions such as, “How many diagonals will different polygons have?”, or “How does the area of a polygon change as its number of sides increases?” Measurement
“Below the line” in the Measure menu, you’ll find commands that will enable students to explore analytic geometry as Descartes did—investigating shapes and solving problems using the Cartesian coordinate system.
Geometric Thinking and ProofAlthough Sketchpad provides a foundation in the visual realm as students work with geometric ideas, it also supports transition from mere visual recognition (van Hiele level 0: visualization); to recognizing properties through construction, vocabulary use, and also through the sheer number of examples available for different shapes (van Hiele level 1: analysis); and then to recognizing relationships among properties through the making and testing of hypothesis, looking for generalizations and counterexamples (van Hiele level 2: abstraction). As students develop skills in geometric thinking and proof, Sketchpad can play an important role in a variety of ways, based on your particular goals. For example, through measurements or dragging, Sketchpad can help students verify results and gain confidence about the validity of conjectures. Sketchpad’s visualization capacities can also help students gain insight into why a relationship is true. And, Sketchpad can help students discover new results, and then communicate their findings in precise, compelling ways (especially using the Marker tool and Hot Text). Sketchpad helps students make geometric objects their own—they construct them, manipulate them, and uncover important relationships. And the geometric tools that they use to explore the geometry curriculum will enable them to model a wide range of mathematical problems, putting their visual and dynamic abilities to work in creating, testing, and communicating solutions. |
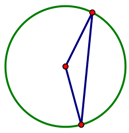 Draw a circle, then use the segment tool to construct two radii and the segment that joins the radius points. The resulting triangle has now been constructed to be an isosceles triangle, not just drawn to look like one! Encourage students to always drag their constructions to make sure they behave as they should. Sketchpad will provide instant feedback—students can use the “drag test” to check their own work, rather than relying on you to evaluate it.
Draw a circle, then use the segment tool to construct two radii and the segment that joins the radius points. The resulting triangle has now been constructed to be an isosceles triangle, not just drawn to look like one! Encourage students to always drag their constructions to make sure they behave as they should. Sketchpad will provide instant feedback—students can use the “drag test” to check their own work, rather than relying on you to evaluate it.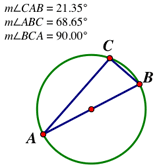 The Measure menu offers valuable tools for exploring geometry, with commands for perimeter, circumference, area, length, distance, angle, radius, and ratio. Consider a triangle ABC, where AB is the diameter of a circle and C is on the circumference. Students can measure all three angles; when C is dragged along the circumference, angles B and C vary, while angle C always measures 90°. Ask students to change the size of the circle and check whether the measurement of angle C still stays the same. By using measurements, students can begin to appreciate the importance of invariance in geometry, and to look for examples of it in their own investigations.
The Measure menu offers valuable tools for exploring geometry, with commands for perimeter, circumference, area, length, distance, angle, radius, and ratio. Consider a triangle ABC, where AB is the diameter of a circle and C is on the circumference. Students can measure all three angles; when C is dragged along the circumference, angles B and C vary, while angle C always measures 90°. Ask students to change the size of the circle and check whether the measurement of angle C still stays the same. By using measurements, students can begin to appreciate the importance of invariance in geometry, and to look for examples of it in their own investigations.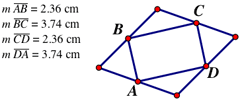 Measurement is an important tool in conjecture. For example, when students connect the midpoints of a rhombus with segments, they may conjecture that the resulting quadrilateral is a rectangle. Finding measures can quickly support or contradict emerging hypotheses, saving students time in pursuing false paths. If conjectures are supported by measurement and the “drag test,” the next step is answering the question, “Why?” Sketchpad can help there too...
Measurement is an important tool in conjecture. For example, when students connect the midpoints of a rhombus with segments, they may conjecture that the resulting quadrilateral is a rectangle. Finding measures can quickly support or contradict emerging hypotheses, saving students time in pursuing false paths. If conjectures are supported by measurement and the “drag test,” the next step is answering the question, “Why?” Sketchpad can help there too...